Barisan Dan Deret

Disini Bimbel Jakarta Timur akan menjelaskan secara rinci dan jelas tentang Barisan dan Deret. Barisan bilangan itu adalah bilangan yang tersusun menurut aturan tertentu, sehingga suku-sukunya merupakan fungsi dari n, n ∈ bilangan asli

Barisan aritmatika adalah suatu barisan dengan selisih atau beda antara dua suku yang berurutan selalu tetap.

Barisan geometri adalah suatu barisan dengan rasio (pembanding/pengali) antara dua suku yang berurutan selalu tetap.

Deret bilangan adalah penjumlahan dari suku-suku barisan

Barisan Dan Deret Aritmatika

Ciri dari barisan aritmatika adalah beda atau selisih dari dua suku berurutan selalu tetap.

a  =suku pertama

b  =beda

Un=suku ke-n

Sn=jumlah n suku pertama

Barisan Aritmatika

Jika di antara bilangan a dan p disisipkan n buah bilangan dan membentuk sebuah barisan/deret aritmatika, maka beda barisan/deret tersebut adalah: b=(p -a)/(n+1).

Untuk n ganjil, maka suku tengahnya (Ut) adalah : Ut=(a+ Un)/2

Un=Sn - Sn-1

Barisan Dan Deret Geometri

Ciri dari barisan geometri adalah rasio (pembanding/pengali) antara dua suku yang berurutan selalu tetap.

a  =suku pertama

r  =rasio

Un=suku ke-n

Sn=jumlah n suku pertama

Untuk n ganjil, maka suku tengahnya (Ut) adalah : Ut=√(a.Un)

Barisan Geometri

Deret geometri tak hingga adalah deret geometri yang penjumlahanya sampai suku tak hingga.

Deret geometri mempunyai jumlah/limit/konvergen jika -1 < r < 1

Deret Geometri

Contoh Soal Dan Pembahasan

1. Tentukan 3 suku berikutnya dari barisan  5, 8, 11, 14,...

Penyelesaian :

Pola barisan bilangan diatas adalah bertambah 3 dari sulu sebelumnya.

Jadi 3 suku berikutnya dari barisan bilangan di atas adalah 17, 20, 23

2. Tentukan 3 suku pertama dari barisan yang ditentukan Un=3n - 5

Penyelesaian :

Substitusi n=1,2,3

Un=3n - 5

U1=3.1 - 5=-2

U2=3.2 - 5= 1

U3=3.3 - 5= 4

Jadi 3 suku pertama dari barisan tersebut adalah -2, 1, 4

3. Tentukan rumus suku ke-n dari barisan bilangan 5, 9, 13, 14, ...

Penyelesaian :

Suku pertama a=5

Beda barisan=U2 -U1=4

Un=a + (n - 1)b

Un=5 + (n - 1).4=5 + 4n - 4

Un=4n + 1

4. Hitung jumlah 6 suku pertama dari 3, 8, 13, 18,...

Penyelesaian :

a=3, b=5, n=6

Sn=n/2 [2a + (n - 1).b]

Sn=6/2 [2.3 + (6-1).5]  =3 (6+25)=3. 31=93 

5. Suku ke 3 dan suku ke 7 suatu barisan aritmatika berturut-turut adalah 8 dan 28. Tentukan jumlah 10 suku pertama barisan tersebut!

Penyelesaian :

U3=a + (3-1)b=a + 2b= 8

U7=a + (7-1)b=a + 6b=28  -

                                -4b=-20

                                   b=5

cara cepat b=U7 - U3

                           7 - 3 

a + 2b=8

a + 2.5=8

a + 10=8

a=8-10=-2

Sn=n/2 [2a + (n - 1).b]

Sn=10/2 [2.(-2) + (10 -1).5]=5 [-4 + 45]=5 . 41=205

6. Jumlah n suku pertama suatu deret aritmatika adalah Sn=n² + 3n. Suku kelima barisan tersebut adalah...

Penyelesaian :

Un=Sn - Sn-1 =S5 - S4

    =[ 5² + 3.5] - [4² + 3.4]

    =[25 + 15] - [16 + 12]

    =40 - 28=12

7. Di antara bilangan 9 dan 111 disisipkan sebanyak 33 bilangan, sehingga bilangan semula dan bilangan-bilangan yang disisipkan membentuk barisan aritmatika. Tentukan suku kedua puluh satu barisan tersebut adalah....

Penyelesaian :

b=(111 - 9)/ (33+1)=102/34=3

Un=a + (n-1)b=9 + (21-1).3=9 + 60=69

8. Jumlah n suku pertama suatu barisan aritmatika dirumuskan dengan Sn=n² -3n. Maka suku ke-10 barisan tersebut adalah...

Un=Sn - Sn-1

U10=S10 - S9

      =(10² -3.10) - (9² -3.9)

      =(100 -30) - (81-27)

      =70 - 54=16

9. Tentukan suku ke-n dari barisan berikut 4,12, 36, 108, ...

Penyelesaian :

a=4, r=12/4=3

Un=a.r^n-1

Un=4.3n-1

10. Tiga bilangan membentuk barisan geometri. Jika hasil kali ketiga bilangan adalah 8.000, dan jumlah bilangan terkecil dan terbesar adalah 104. Maka rasio barisan tersebut adalah...

Penyelesaian :

U1.U2.U3=8.000

a.ar.ar²=8.000

a³r³=8.000

(ar)³=20³

ar=20, a=20/r

a + ar²=104

a (1+ r²)=104

20/r (1+r²)=104

20 (1+r²)=104.r

20 + 20r²=104r

20r² - 104r + 20=0..... (:) 4

5r² - 26r + 5=0

(5r -1) (r-5)=0

r=1/5 atau r=5

11. n - 1, n + 2, 3n adalah tiga suku pertama suatu barisan geometri. Jika n adalah bilangan

bulat positif, tentukanlah suku ke-empat barisan tersebut.

Penyelesaian :

ciri barisan geometri adalah rasio, dimana r=U2/U1=U3/U2=U4/U3 ....

maka U2/U1=U3/U2

(n+2)/(n-1)=3n/(n+2).... kali silang

(n+2)(n+2)=3n(n-1)

n²+4n+4=3n² -3n

0=3n² -n² -3n - 4n - 4

0=2n² - 7n -4

0=(2n+1) (n-4)

2n+1=0

n=-1/2 (tidak memenuhi)

n-4=0

n=4 (memenuhi)

maka suku pertama adalah n-1=4-1=3

rasio adalah U2/U1=(n+2)/(n-1)=(4+2)/(4-1)=2

U4=a.r³

=3.2³=3.8=24

12. Suatu barisan geometri terdiri dari lima suku. Jika suku pertama barisan tersebut adalah 4

dan suku terakhirnya adalah 256, tentukan suku ke-3 barisan geometri tersebut.

Penyelesaian :

a=4, U5=256

Un=a.rn-1

U5=a.r⁴

256=4.r⁴

r⁴ =256/4=64

r=∜64

r=2√2

U3=a.r²

    =4.(2√2)²

    =4.8=32

13. .Diketahui deret geometri 3 + 3² + 3³ + ...+ 3n =363. Banyaknya suku pada deret tersebut adalah...

Penyelesaian :

a=3, r=3, Sn=363

Sn      =a(.rn-1)/ (r-1)

363      =3( 3n  -1)/(3-1)

363      =3( 3n  -1)/2

363.2/3=  3n  -1

242      = 3n -1

243       = 3n 

n          =5

14. Suku ke-2 dan suku ke-5 suatu barisan geometri adalah 14 dan 112. Suku ke enam barisan geometri tersebut adalah...

Penyelesaian :

U2=a.r=14

U5=a.r⁴ =112

     ar.r³=112

     14..r³=112

     .r³=112/14=8

      r=∛8=2

ar  =14

a.2=14

a    =14/2=7

U6=a.r⁵

    =7.2⁵

    =7.32

    =224

15. Tiga bilangan membentuk barisan geometri naik. Hasil kali dan jumlah bilangan tersebut berturut-turut adalah 512 dan 28. Suku ketiga barisan tersebut adalah...

Penyelesaian :

Hasil kali adalah  512

U1.U2.U3        =512

(U2/r)(U2)(U2.r) =512

(U2)³                =512

U2                  =∛512=8

Jumlah adalah 28

U1 + U2 + U3=28

U2/r + U2 + U2.r=28

8/r + 8 + 8r=28 

8r - 20 + 8/r=0 .... (x) r/4

2r² -5r + 2=0

(2r-1)(r-2)=0

2r-1=0

2r=1

r=1/2, atau

r-2=0

r=2

Karena barisan tersebut adalah barisan geometri naik maka r=2

U3=U2.r=8.2=16

16. Jumlah tak hingga suatu deret geometri adalah 48, sedangkan jumlah suku-suku bernomor genapnya sama dengan 16. Berapakah rasio dari deret geometri tersebut?

Penyelesaian :

Sganjil + Sgenap=S∽

Sganjil + 16=48

Sganjil=48 - 16=32

r=Sgenap  =16 =1

     Sganjil       32    2

17. Diketahui suatu deret geometri tak hingga 3 + 1,5 + 0,75 ....

Tentukanlah Jumlah tak hingga suku ganjil deret tersebut !

Penyelesaian :

a=3, 

r=1,5/3=0.5

Sganjil=   a      

              1 - r²

        =   3   

              1-0,5²

        =   3   

               0,75

        =4

18. Pada bulan pertama Daffa menabung sebesar Rp 150.000,00, pada bulan kedua Rp 170.000,00 demikian seterusnya tiap bulan jumlah yang ditabung bertambah Rp 20.000,00. Besar tabungan Daffa setelah 1 tahun adalah...

Penyelesaian :

a=150.000

b= 20.000

n=12 bulan

S12=12/2 (2x150.000 + (12-1) 20.000)

      =6 (300.000 + 220.000)

      =6 (420.000)

      =2.520.000

Jadi jumlah seluruh tabungan Daffa selama 1 tahun adalah Rp 2.520.000,00

19. Seutas tali dibagi menjadi enam potong dengan tiap bagiannya membentuk barisan geometri. Jika potongan terpendek adalah 2 cm dan potongan terpanjang adalah 486 cm, maka panjang tali semula adalah...

Penyelesaian :

a=2

U6  =486

a.r⁵  =486

2..r⁵ =486

r⁵      =486/2=243

r      =3

S6=a (r⁶ -1)

           r-1

    = 2(3⁶ -1)

           3-1

    = 2 (729-1)

             2

    =728

20. Sebuah bola dijatuhkan ke lantai dari tempat yang ketinggiannya 1,5 meter. Setiap kali bola memantul, bola mencapai ketinggian yang sama dengan 2/3 dari ketinggian yang dicapai sebelumnya. Panjang lintasan bola sejak dilemparkan sampai terhenti adalah...

Penyelesaian :

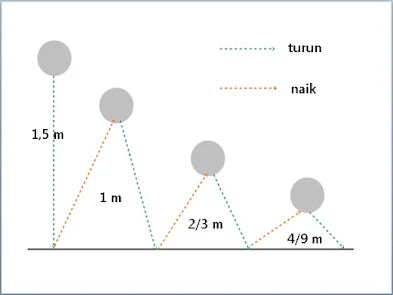Soal Nomer 20

  Sturun=1,5 + 1 +2/3 + 4/9 + ... 

            =  a     =  1,5    =  1,5    =4,5

                1-r       1-2/3        1/3

Snaik=1 + 2/3 + 4/9 +...

          =   a     =   1    =   1    =3

              1-r      1-2/3     1/3

Panjang lintasan=Sturun + Snaik=4,5 + 3=7,5 m